以前好几次在学语言的使用都有实现这个ack函数的经历,今天读本算法书,偶尔又提到了这个,查了下wiki来头好大
| m\n | 0 | 1 | 2 | 3 | 4 | n |
|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 |  |
| 1 | 2 | 3 | 4 | 5 | 6 | 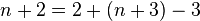 |
| 2 | 3 | 5 | 7 | 9 | 11 | 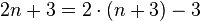 |
| 3 | 5 | 13 | 29 | 61 | 125 |  |
| 4 | 13= | 65533= | 265536 − 3= |  = = |  = = |  |
本文共 229 字,大约阅读时间需要 1 分钟。
以前好几次在学语言的使用都有实现这个ack函数的经历,今天读本算法书,偶尔又提到了这个,查了下wiki来头好大
| m\n | 0 | 1 | 2 | 3 | 4 | n |
|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 |  |
| 1 | 2 | 3 | 4 | 5 | 6 | 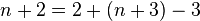 |
| 2 | 3 | 5 | 7 | 9 | 11 | 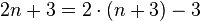 |
| 3 | 5 | 13 | 29 | 61 | 125 |  |
| 4 | 13= | 65533= | 265536 − 3= |  = = |  = = |  |
转载于:https://www.cnblogs.com/lailailai/p/3584600.html